Chương 01

Cơ bản về mạng nơ-ron nhân tạo

Mạng nơ-ron nhân tạo (Artificial Neural Network - ANN) là một thuật toán học tập có giám sát được lấy cảm hứng từ cách thức hoạt động của bộ não con người. Tương tự như cách nơ-ron được kết nối và kích hoạt trong não người, mạng nơ-ron nhận đầu vào và chuyển nó qua hàm chức năng, dẫn đến một số nơ-ron tiếp theo được kích hoạt và do đó tạo ra đầu ra. Đối với một tập dữ liệu/tác vụ nhất định, ta có thể tạo một kiến trúc và tiếp tục điều chỉnh trọng số của nó cho đến khi ANN dự đoán những gì mong muốn. Việc điều chỉnh các trọng số này được gọi là huấn luyện mạng thần kinh.

Trong chương này, một kiến trúc mạng nơ-ron rất đơn giản sẽ được xây dựng trên một tập dữ liệu đơn giản và chủ yếu tập trung vào cách các khối xây dựng khác nhau (feedforward, backpropagation, learning rate) của ANN giúp điều chỉnh trọng số để mạng học cách dự đoán kết quả đầu ra mong đợi từ các đầu vào đã cho. Những chủ đề sau sẽ được đề cập đến:

• Tìm hiểu về các khối xây dựng nên một ANN.
• Thực hiện feedforward propagation.
• Thực hiện backpropagation.
• Kết hợp feedforward propagation và backpropagation.
• Hiểu về sự ảnh hưởng của learning rate trong việc huấn luyện.
• Tóm tắt quá trình huấn luyện mạng nơ-ron.

Tìm hiểu về các khối xây dựng nên một mạng nơ-ron nhân tạo

ANN là một tập hợp các tensor (trọng số) và các phép toán. Nó có thể được xem như một hàm toán học nhận một hoặc nhiều tensor đầu vào và dự đoán một hoặc nhiều tensor đầu ra. Việc sắp xếp các phép tính kết nối các đầu vào và đầu ra được gọi là kiến trúc của mạng nơ-ron. Chúng ta có thể tùy chỉnh kiến trúc của mạng nơ-ron dựa trên nhiệm vụ hiện tại. Một ANN được tạo thành từ những phần sau:

• Các lớp đầu vào: Các lớp này lấy các biến độc lập làm đầu vào.
• Các lớp ẩn (trung gian): Các lớp này kết nối các lớp đầu vào và đầu ra trong khi thực hiện các phép biến đổi trên đầu dữ liệu đầu vào. Hơn nữa, các lớp ẩn chứa các nút (vòng tròn trong sơ đồ sau) để biến đổi các giá trị đầu vào của chúng thành các giá trị có chiều cao hơn/thấp hơn. Chức năng để đạt được một biểu diễn phức tạp hơn đạt được bằng cách sử dụng các hàm kích hoạt khác nhau để biến đổi các giá trị của các nút của các lớp trung gian.
• Lớp đầu ra: Lớp này chứa các giá trị mà các biến đầu vào dự kiến sẽ tạo ra.

Với suy nghĩ này, cấu trúc điển hình của một mạng lưới thần kinh như sau:

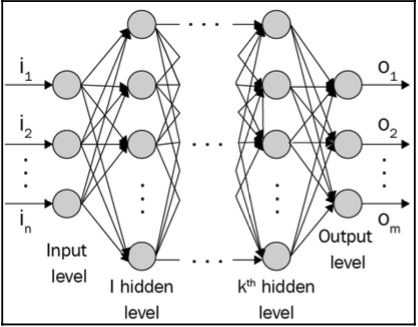
Số lượng nút của lớp đầu ra phụ thuộc vào nhiệm vụ đang thực hiện và việc chúng ta đang muốn dự đoán một biến liên tục hay một biến phân loại. Nếu đầu ra là một biến liên tục, đầu ra có một nút. Nếu đầu ra là phân loại với $m$ lớp, thì sẽ có $m$ nút trong lớp đầu ra. Một nơ-ron biến đổi đầu vào của nó như sau:

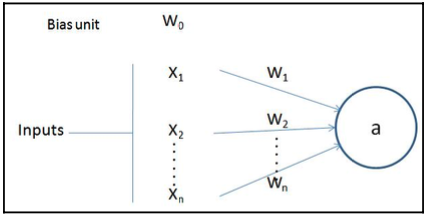
Ở sơ đồ trước, $x_1, x_2,\ldots, x_n$ là các biến đầu vào, và $w_0$ số hạng sai lệch (tương tự như cách chúng ta có sai lệch trong hồi quy tuyến tính).

Lưu ý rằng $w_1, w_2,\ldots, w_n$ là các trọng số được cung cấp cho mỗi biến đầu vào và $w_0$ là số hạng sai lệch. Giá trị đầu ra $a$ được tính như sau:

$$a = f\left(w_0 + \sum_{i=1}^nw_ix_i\right)\nonumber$$

Hàm $f$ là hàm kích hoạt được sử dụng để áp dụng tính phi tuyến tính.

Mạng thần kinh là tập hợp các nút trong đó mỗi nút có giá trị thực có thể thay đổi và các nút được kết nối với nhau dưới dạng biểu đồ. Mạng được cấu thành bởi ba phần chính: lớp đầu vào, (các) lớp ẩn và lớp đầu ra. Lưu ý rằng bạn có thể có số lượng (n) lớp ẩn cao hơn, với thuật ngữ học sâu (deep learning - DL) đề cập đến số lượng lớp ẩn lớn hơn. Thông thường, cần có nhiều lớp ẩn hơn khi mạng nơ-ron phải học điều gì đó phức tạp, chẳng hạn như nhận dạng hình ảnh.

Sau khi đã hiểu kiến trúc của mạng thần kinh, trong phần tiếp theo, chúng ta sẽ tìm hiểu về feedforward propagation, giúp ước lượng mức độ lỗi (mất mát) của kiến trúc.

Thực hiện feedforward propagation

Để xây dựng hiểu biết cơ bản vững chắc về cách thức hoạt động của quá trình truyền theo chiều ngược, chúng ta sẽ xem qua một ví dụ đồ chơi về huấn luyện mạng nơ-ron trong đó đầu vào của mạng nơ-ron là (1, 1) và đầu ra (dự kiến) tương ứng là 0. Ở đây, chúng ta sẽ tìm các trọng số tối ưu của mạng thần kinh dựa trên cặp đầu vào-đầu ra duy nhất này. Tuy nhiên, bạn cần lưu ý rằng trên thực tế, sẽ có hàng nghìn điểm dữ liệu mà ANN được đào tạo.

Kiến trúc mạng thần kinh của chúng tôi cho ví dụ này chứa một lớp ẩn với ba nút trong đó, như sau:

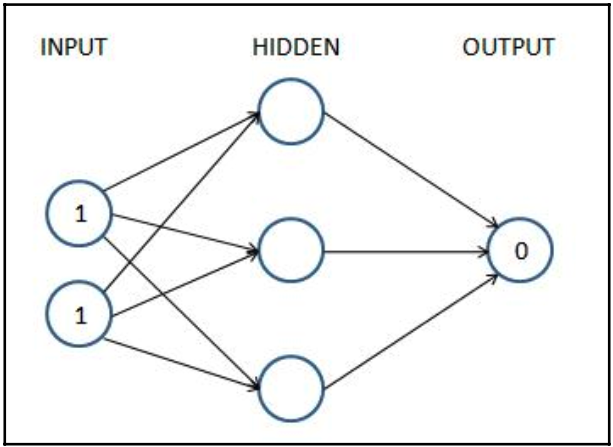
Mỗi mũi tên trong sơ đồ trước chứa chính xác một giá trị float (trọng lượng) có thể điều chỉnh được. Có 9 (6 ở lớp ẩn đầu tiên và 3 ở lớp thứ hai) mà chúng ta cần tìm, sao cho khi đầu vào là (1,1) thì đầu ra càng gần (0) càng tốt. Đây là những gì chúng tôi muốn nói bằng cách đào tạo mạng lưới thần kinh. Chúng tôi chưa giới thiệu giá trị sai lệch, chỉ vì mục đích đơn giản – logic cơ bản vẫn giữ nguyên.

In the subsequent sections, we will learn the following about the preceding network:

• Tính giá trị lớp ẩn.
• Thực hiện kích hoạt phi tuyến tính.
• Ước tính giá trị lớp đầu ra.
• Tính giá trị tổn thất tương ứng với giá trị kỳ vọng.

Tính toán các giá trị đơn vị lớp ẩn

Bây giờ chúng ta sẽ gán trọng số cho tất cả các kết nối. Trong bước đầu tiên, chúng tôi gán trọng số ngẫu nhiên trên tất cả các kết nối. Và nói chung, các mạng thần kinh được khởi tạo với các trọng số ngẫu nhiên trước khi quá trình huấn luyện bắt đầu. Một lần nữa, để đơn giản, trong khi giới thiệu chủ đề, chúng tôi sẽ không bao gồm giá trị sai lệch khi tìm hiểu về lan truyền tiến và lan truyền ngược. Nhưng chúng tôi sẽ có nó trong khi thực hiện cả truyền bá ngược và truyền ngược từ đầu.

Hãy bắt đầu với các trọng số ban đầu được khởi tạo ngẫu nhiên trong khoảng từ 0 đến 1, nhưng lưu ý rằng các trọng số cuối cùng sau quá trình đào tạo của mạng nơ-ron không cần phải nằm trong một tập hợp giá trị cụ thể. Biểu diễn chính thức của các trọng số và giá trị trong mạng được cung cấp trong sơ đồ sau (nửa bên trái) và các trọng số được khởi tạo ngẫu nhiên được cung cấp trong mạng ở nửa bên phải.

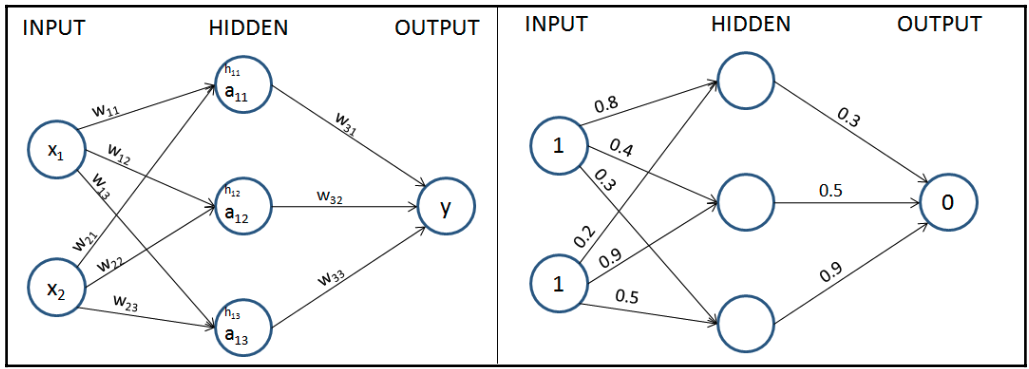
Trong bước tiếp theo, chúng tôi thực hiện phép nhân đầu vào với các trọng số để tính giá trị của các đơn vị ẩn trong lớp ẩn.

Các giá trị đơn vị của lớp ẩn trước khi kích hoạt thu được như sau:

$$\begin{align} h_{11} &= X_1*w_{11} + X_2*w_{21} = 1*0.8+1*0.2=1\\ h_{12} &= X_1*w_{12} + X_2*w_{22} = 1*0.4+1*0.9=1.3\\ h_{13} &= X_1*w_{13} + X_2*w_{23} = 1*0.3+1*0.5=0.8\nonumber \end{align}$$

Các giá trị đơn vị của lớp ẩn (trước khi kích hoạt) được tính toán ở đây cũng được hiển thị trong sơ đồ sau:

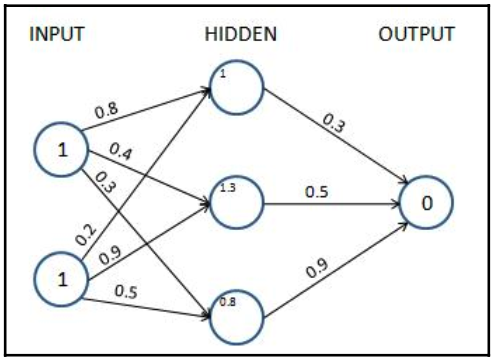
Bây giờ, chúng ta sẽ chuyển các giá trị của lớp ẩn thông qua kích hoạt phi tuyến tính. Lưu ý rằng, nếu chúng ta không áp dụng chức năng kích hoạt phi tuyến tính trong lớp ẩn, mạng thần kinh sẽ trở thành một kết nối tuyến tính khổng lồ từ đầu vào đến đầu ra, bất kể có bao nhiêu lớp ẩn tồn tại.

Áp dụng hàm kích hoạt

Các hàm kích hoạt giúp mô hình hóa các mối quan hệ phức tạp giữa đầu vào và đầu ra.

Một số hàm kích hoạt thường được sử dụng được tính toán như sau (trong đó $x$ là đầu vào):

$$\begin{align} Sigmoid~actavation(x)&=\frac{1}{1+e^{-x}}\\ ReLu~activation(x)&=\left\{\begin{matrix} x\quad \text{if}~x>0\\ 0\quad \text{if}~x\leq0 \end{matrix}\right.\\ Tanh~activation(x) &= \frac{e^x-e^{-x}}{e^x+e^{-x}}\\ Tanh~activation(x) &= x\nonumber \end{align}$$

Hình ảnh của từng kích hoạt trước cho các giá trị đầu vào khác nhau như sau:

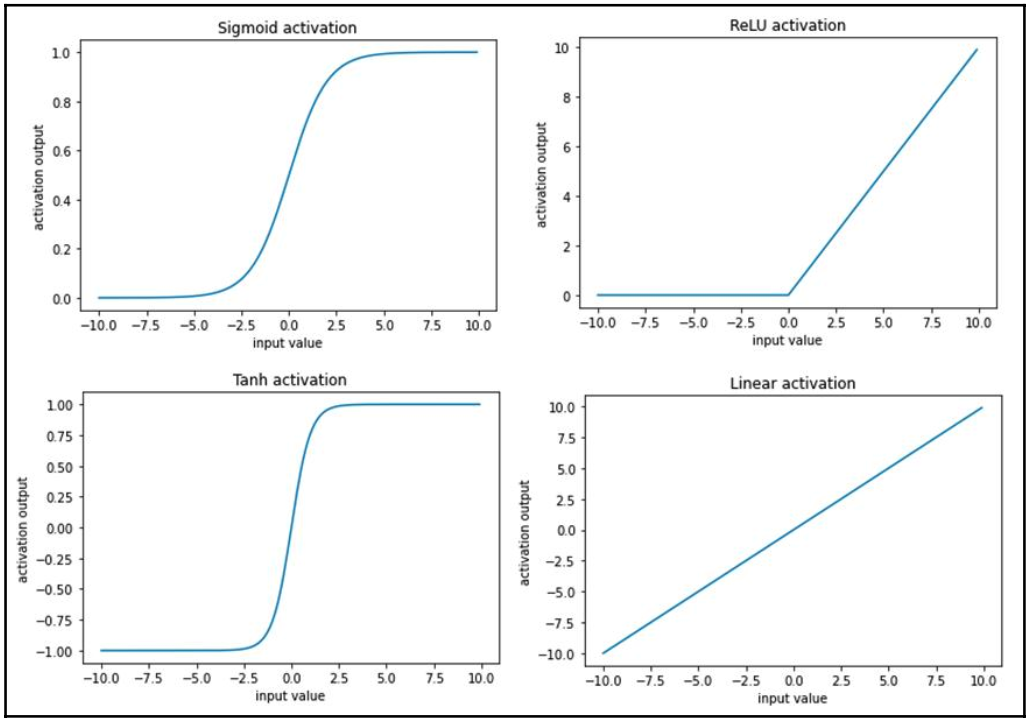
Ví dụ của chúng tôi, hãy sử dụng hàm sigmoid (logistic) để kích hoạt.

Bằng cách áp dụng kích hoạt sigmoid (logistic), $S(x)$, cho tổng ba lớp ẩn, chúng tôi nhận được các giá trị sau sau khi kích hoạt sigmoid:

$$a_{11} = S(1.0) = \frac{1}{1+e^{-1}} = 0.73\\ a_{12} = S(1.3) = \frac{1}{1+e^{-1.3}} = 0.79\\ a_{13} = S(0.8) = \frac{1}{1+e^{-0.8}} = 0.69\nonumber$$

Bây giờ chúng ta đã lấy được các giá trị của lớp ẩn sau khi kích hoạt, trong phần tiếp theo, chúng ta sẽ lấy các giá trị của lớp đầu ra.

Tính toán các giá trị lớp đầu ra

Cho đến nay, chúng tôi đã tính toán các giá trị lớp ẩn cuối cùng sau khi áp dụng kích hoạt sigmoid. Sử dụng các giá trị của lớp ẩn sau khi kích hoạt và các giá trị trọng số (được khởi tạo ngẫu nhiên trong lần lặp đầu tiên), chúng tôi sẽ tính toán giá trị đầu ra cho mạng của mình:

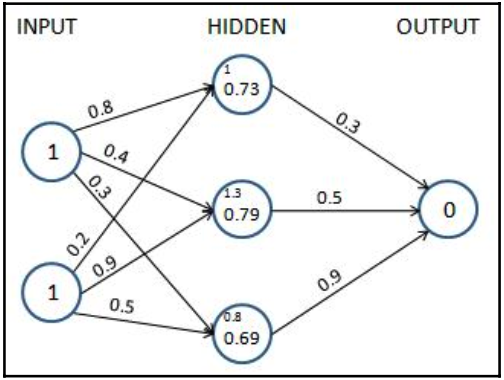
Chúng tôi thực hiện tổng các sản phẩm của các giá trị lớp ẩn và giá trị trọng số để tính giá trị đầu ra. Một lời nhắc khác: chúng tôi đã loại trừ các thuật ngữ sai lệch cần được thêm vào mỗi đơn vị (nút), chỉ để đơn giản hóa hiểu biết của chúng tôi về các chi tiết hoạt động của feedforward propagation và backpropagation và sẽ bao gồm nó trong khi mã hóa lan feedforward propagation và backpropagation:

$$\text{output node value}~(\widehat{y})=0.73*0.3+0.79*0.5+0.69*0.9=1.235\nonumber$$

Bởi vì chúng tôi đã bắt đầu với một tập trọng số ngẫu nhiên, giá trị của nút đầu ra rất khác so với mục tiêu. Trong trường hợp này, sự khác biệt là 1,235 (hãy nhớ rằng, mục tiêu là 0). Trong phần tiếp theo, chúng ta sẽ tìm hiểu về cách tính giá trị tổn thất liên quan đến mạng ở trạng thái hiện tại.

Tính giá trị tổn thất

Giá trị tổn thất (còn được gọi là hàm chi phí) là các giá trị mà chúng tôi tối ưu hóa trong mạng thần kinh. Để hiểu cách tính các giá trị tổn thất, hãy xem xét hai tình huống:

• Dự đoán biến phân loại.
• Dự đoán biến liên tục.

Tính toán tổn thất trong quá trình dự đoán biến liên tục

Thông thường, khi biến là liên tục, giá trị tổn thất được tính bằng giá trị trung bình của bình phương chênh lệch giữa giá trị thực và dự đoán, nghĩa là chúng tôi cố gắng giảm thiểu sai số bình phương trung bình bằng cách thay đổi các giá trị trọng số được liên kết với mạng thần kinh. Giá trị lỗi bình phương trung bình được tính như sau:

$$\begin{align} J_\theta&=\frac{1}{m}\sum_{i=1}^{m}\left ( y_i-\widehat{y}_i \right )^2\\ \widehat{y}_i&=\eta_\theta(x_i)\nonumber \end{align}$$

Trong công thức trước, $y_i$ là giá trị thực của ngõ ra. $\widehat{y}_i$ là giá trị dự đoán được tính bởi mạng nơ-ron $\eta$ (các trọng số của mạng được lưu trữ dạng $\theta$), với giá trị đầu vào là $x_i$, và $m$ là số hàng của tập dữ liệu.

Điều quan trọng cần rút ra là thực tế là đối với mỗi tập trọng số duy nhất, mạng nơ-ron sẽ dự đoán một tổn thất khác nhau và chúng ta cần tìm tập trọng số vàng mà tổn thất bằng 0 (hoặc, trong các tình huống thực tế, gần bằng 0 càng tốt).

Trong ví dụ của chúng tôi, hãy giả sử rằng kết quả mà chúng tôi dự đoán là liên tục. Trong trường hợp đó, giá trị hàm mất mát là sai số bình phương trung bình, được tính như sau:

$$loss(error)=1.235^2=1.52\nonumber$$

Bây giờ chúng ta đã hiểu cách tính giá trị tổn thất cho biến liên tục, trong phần tiếp theo, chúng ta sẽ tìm hiểu về cách tính giá trị tổn thất cho biến phân loại.

Tính toán tổn thất trong dự đoán biến phân loại

Khi biến để dự đoán là rời rạc (nghĩa là chỉ có một vài loại trong biến), chúng ta thường sử dụng hàm mất entropy chéo phân loại. Khi biến để dự đoán có hai giá trị riêng biệt bên trong nó, thì hàm mất mát là cross-entropy nhị phân.

Binary cross-entropy is calculated as follows:

$$-\frac{1}{m}\sum_{i=1}^{m}\left ( y_i\log(p_i) + (1-y_i)\log(p_i) \right )$$

$y$ là giá trị thực của ngõ ra, $p$ là giá trịc dự đoán của ngõ ra, và $m$ là tổng số mẫu của dữ liệu.

Cross-entropy phân loại được tính như sau:

$$-\frac{1}{m}\sum_{i=1}^{m}\sum_{j=1}^{C}y_{ji}\log(p_{ji})$$

$y$ là giá trị thực của ngõ ra, $p$ là giá trịc dự đoán của ngõ ra, và $m$ là tổng số mẫu của dữ liệu.

Một cách đơn giản để hình dung sự mất entropy chéo là nhìn vào chính ma trận dự đoán. Giả sử bạn đang dự đoán năm lớp – Chó, Mèo, Chuột, Bò và Gà mái – trong một bài toán nhận dạng hình ảnh. Mạng nơ-ron nhất thiết phải có năm nơ-ron ở lớp cuối cùng với kích hoạt softmax (thêm về softmax trong phần tiếp theo). Do đó, nó sẽ buộc phải dự đoán xác suất cho mọi lớp, cho mọi điểm dữ liệu. Giả sử có năm hình ảnh và xác suất dự đoán giống như vậy (ô được đánh dấu trong mỗi hàng tương ứng với lớp mục tiêu):

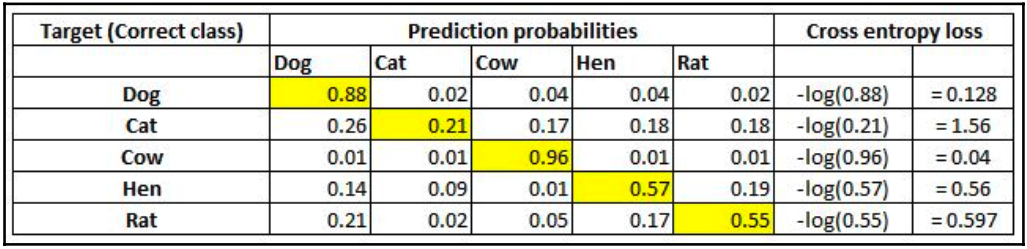
Lưu ý rằng mỗi hàng có tổng bằng $1.$ Ở hàng đầu tiên, khi mục tiêu là Chó và xác suất dự đoán là $0.88$, thì tổn thất tương ứng là $0.128$ (là giá trị âm của log của $0.88$). Tương tự, các tổn thất khác được tính toán. Như bạn có thể thấy, giá trị tổn thất sẽ ít hơn khi xác suất chọn đúng loại cao. Như bạn đã biết, xác suất nằm trong khoảng từ $0$ đến $1$. Vì vậy, tổn thất tối thiểu có thể là $0$ (khi xác suất là $1$) và tổn thất tối đa có thể là vô cùng khi xác suất bằng $0$.

Tổn thất cuối cùng trong tập dữ liệu là giá trị trung bình của tất cả các tổn thất riêng lẻ trên tất cả các hàng.

Bây giờ chúng ta đã hiểu rõ về việc tính toán tổn thất trung bình bình phương sai số và mất mát cross-entropy, hãy quay lại ví dụ của chúng ta. Giả sử đầu ra của chúng ta là một biến liên tục, chúng ta sẽ tìm hiểu cách giảm thiểu giá trị tổn thất bằng cách sử dụng lan truyền ngược trong phần sau. Chúng tôi sẽ cập nhật các giá trị trọng số $\theta$ (được khởi tạo ngẫu nhiên trước đó) để giảm thiểu tổn thất ($J_\theta$)

Tuy nhiên, trước đó, trước tiên chúng ta hãy lập trình feedfoward propagation trong Python bằng cách sử dụng mảng NumPy để củng cố hiểu biết của chúng ta về các chi tiết hoạt động của nó.

Feedforward propagation in code

Các bước thực hiện feedfoward propagation như sau:

1. Thực hiện tổng của tích tại mỗi nút.
2. Áp dụng hàm kích hoạt.
3. Thực hiện lại hai bước trên với các nút còn lại cho đến lớp ngõ ra.
4. Tính sai số bằng cách so sánh giá trị dự đoán và giá trị thực của ngõ ra.

Nó sẽ là một hàm lấy dữ liệu đầu vào, trọng số mạng thần kinh hiện tại và dữ liệu đầu ra làm đầu vào cho hàm và trả về sự mất mát của trạng thái mạng hiện tại.